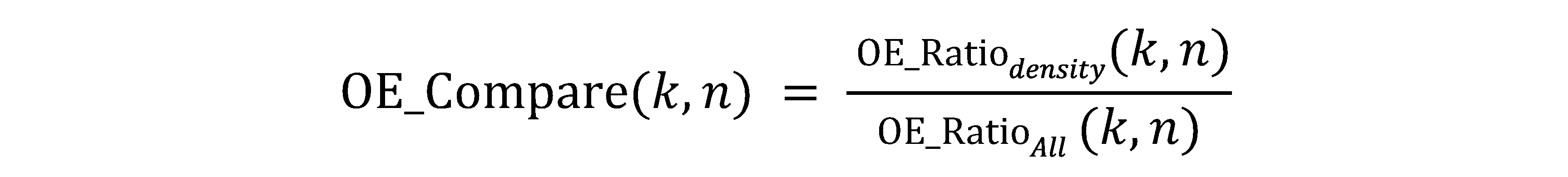OE_Ratio(k,n) can describe the ratio between Observe(k,n) and Expect(k,n) on the same characteristic metric, represents the actual frequency of occurrence of CpG on this metric compared with the frequency of occurrence in the random case. It is also defined that if OE_Ratio(k,n) is greater than 1, we describe OE_Ratio as a positive state representing the actual exceeding of the random case, noted as Positive_state(k,n); otherwise, OE_Ratio is described as a negative state representing the actual below random case, noted as Negative_state(k,n).

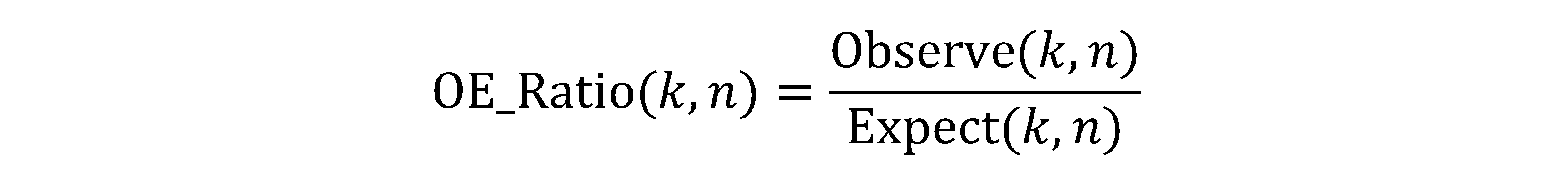
Here, Observe (k, n) is the number of k-mer(s) that consist of an n number of CpGs for each k. Here, n is the number of CpGs in a k-mer, and k is the length of a k-mer.

Expect (k, n) is the number of k-mer(s) that consist of an n number of CpGs for each k in the random condition. OE_Ratio (k, n)：The ratio between Observe (k, n) and Expect (k, n).

Finally, OE_compare(k, n) represents the ratio of OE_Ratio(k,n) for three different densities of CGI divided by all densities of CGI for the same k, n values: